エヤリーの定理について

振幅運動をしているテンプが、外部からの衝撃を受けた時、その出来事は等時性へどのような影響を与えるのでしょうか？
つまり、ショックを受けた時計は、どういう理由で時間が狂うのでしょうか？


●エヤリーの定理

テンプの振り石が、振幅のときに描く円を想像してみてください。
理解のしやすさを考えて、この円を分度器のように区切り、各方向を示せるようにしましょう。
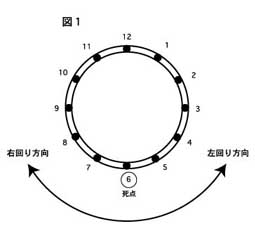
円を時計の文字盤のごとく１〜１２に区切ります。

各方向を示すときには、「１時方向、９時方向」あるいは、「１時、９時」などという言い方にします。
また、回転の方向を右まわり方向（時計まわり方向）と左まわり方向（反時計まわり方向）という言い方をします。
さらに、６時方向は振幅運動の弧の真ん中になるので、死点と言います。

ガリレオ・ガリレイの ”振子の等時性” の法則に照らし合わせると、
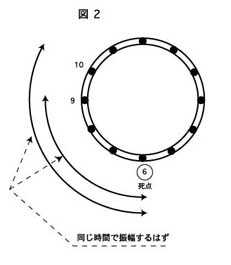
６時から９時までのテンプの振幅速度と、６時から１０時までのテンプの振幅速度は同じであるはずです。

つまり、テンプの勢いが９時方向まで回る自由運動であっても、更に勢い良く１０時方向まで回る自由運動であっても、６時から９時および１０時を描く弧の振幅速度は同じであるはずです。

衝撃

さて、
今、テンプは振幅運動をしていて、１時方向から１１時方向の間を往復しているものとします。
アンクルは６時方向（死点）にあると仮定します。

テンプが１時を出発して５時の位置にきた時、突然、外部から右まわり方向の力を受けたとしましょう。
この死点に到達する前に受ける右まわり方向の力（テンプが回転する方向に向かった力）のことを 衝撃と呼びます。

テンプが５時の位置で回転方向に沿った、順方向の力（衝撃）を受けた訳ですから、当然いつもより早く６時の位置に到達することでしょう。
つまり、５時から６時まで移動する時間が短縮されることでしょう　→ 出来事Ａ
この後、
いつもなら１１時まで回転するテンプが、勢い余ってたとえ１２時まで回転したとしても、自由運動の等時性の法則にのっとって考えると、６時〜１２時を描く弧の振幅速度は、６時〜１１時を描く弧のそれと等しいはずです。

さて、衝撃によって先述した出来事Ａが生じたわけですが、もし衝撃が起こらなかったときと比べて考えてみると、

次のような結論をもってくることができます。

１ テンプが死点に到達する前に衝撃を受けた場合、一往復の時間は短縮される

●抵抗

さて、先ほどは５時地点で右まわり方向（衝撃）の外力を受けたときの考察でしたが、左まわり方向（テンプが回転する方向の逆方向に向かった力）を受けるとどうなるでしょう？
この死点に到達する前に受ける左まわり方向の力（テンプの回転方向の逆方向の力、妨害力）のことを抵抗と呼びます。

テンプが５時の位置で逆方向（抵抗）を受けた訳ですから、当然いつもより遅く６時の位置に到達することでしょう。
つまり、５時から６時まで移動する時間が延長されることでしょう　→ 出来事Ｂ
この後、
いつもなら１１時まで回転するテンプの勢いがなくなって、たとえ１０時までしか回転しなかったとしても、自由運動の等時性の法則にのっとって考えると、６時〜１０時を描く弧の振幅速度は、６時〜１１時を描く弧のそれと等しいはずです。

さて、抵抗によって先述した出来事Ｂが生じたわけですが、もし抵抗が起こらなかった時と比べて考えてみると、

次のような結論をもってくることができます。

２ テンプが死点に到達する前に抵抗を受けた場合、一往復の時間は延長される

●テンプが死点を通過した以降の衝撃と抵抗

これまで、死点前の衝撃と抵抗をみてきましたが、テンプが死点を通過した後に衝撃、抵抗を受けたらどういうことになるでしょうか？

テンプが順調に１時から動いてきて、６時（死点）を通過し、１１時に近づいてきたとします。
この時に右まわり方向の力（衝撃）を受けると、外力を受けたテンプは１２時まで回るかもしれません。
明らかに、１１時〜１２時までの余分の時間が費やされたことになります。

あるいは、
テンプが順調に１時から動いてきて、６時（死点）を通過し、１１時に近づいてきたとします。
この時に左まわり方向の力（抵抗）を受けると、外力を受けたテンプは１０時までしか回らないかもしれません。
明らかに、１０時〜１１時までの運動の時間が短縮されたことになります。

以上のことから次のような結論をもってくることができます。

３ テンプが死点を通過した後に衝撃を受けた場合、一往復の時間は延長される
４ テンプが死点を通過した後に抵抗を受けた場合、一往復の時間は短縮される

死点の通過前と後では結果が全く逆になるわけですね。

まとめると次のようになります。

死点前の衝撃 → 進み
死点前の抵抗 → 遅れ
死点後の衝撃 → 遅れ
死点後の抵抗 → 進み

以上をエヤリーの定理といいます。

●外力がテンプに影響を与える具合

テンプが、外力（衝撃・抵抗）によってどの程度速度を変えるかは、テンプの慣性モーメント（以下に注あり）によって変わってきます。
径の大きい重いテンプは慣性モーメントが大きいので外力の影響を受けにくいです。
同じ慣性モーメントのテンプであれば、テンプの速度が速いほど外力の影響を受けにくいです。


まとめると

外力は、その力が強いほど、その力が長時間働くほど、テンプの慣性モーメントが小さいほど、テンプの速度が小さいほど、テンプに与える影響が大きくなります。

●慣性モーメント

小さいトロッコと大きい電車が等速度で走っている場合、この二つを停止させるのにはどちらが大きな力を必要とするでしょう？

もちろん、大きな電車ですね。
動いている物体はそのまま動き続けようとしますが、それを止める力は、その物体の重量に大きく関わってくるのです。

次に、円運動を考えてみましょう。
同じ重量の円柱と円盤があるとします。
重量は同じですが、半径が違います。
円盤の方が円柱よりも半径が大きいのです。
この両者が軸を中心にして等速度で回転しているとして、その回転を止めるのには、どちらが大きな力を必要とするでしょう？

答えは、円盤の方が止めるのに大きな力がいるのです。

慣性は形状によっても違ってきます。
回転体の慣性は、回転体を構成する重量が、中心軸の近くにあるか、遠くにあるかによっても変わってきます。
回転体の慣性を慣性モーメントといい、それは回転体の重量と形状に関係しています。